单变量的线性回归模型(linear regression model)是监督学习中最简单的一个基本模型。
在处理回归问题时，数据可能会出现线性结构。此时可以利用一元线性回归模型构建模型回归线。
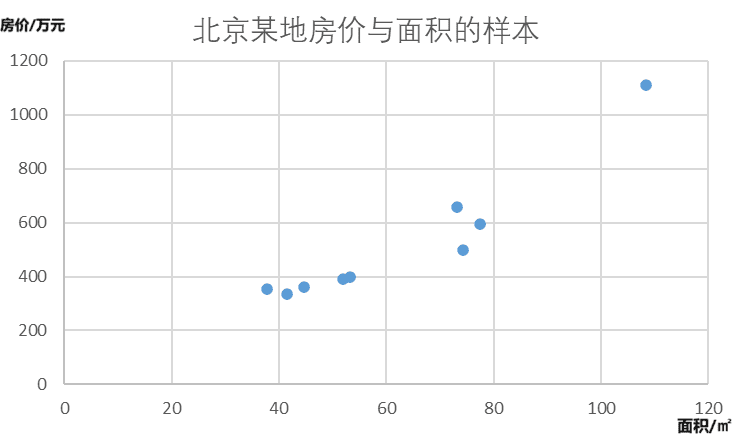
我们可以将feather和label作为x、y轴建立坐标系。在该坐标系中的一条直线可以用一元一次方程表示。
y=wx+b
只要找对了方程中的w值和b值，就能够找出模型的一条回归线。可以通过取任意的w，b值得到无数条直线。我们先任取一条直线为例。
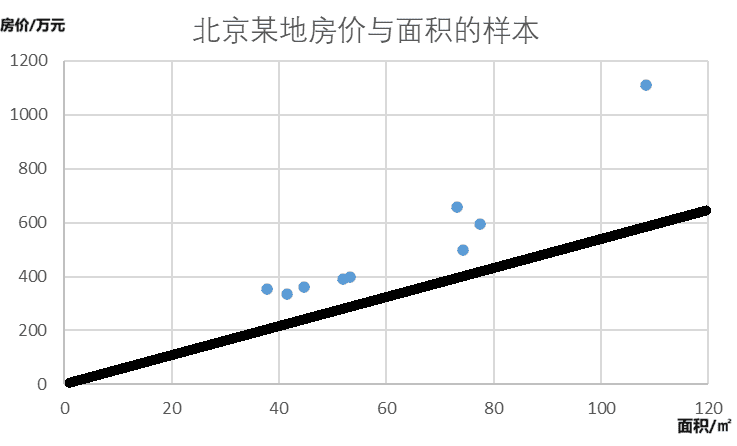
判断这条直线是否为最符合样本（sample）的回归线就需要引入代价函数（cost function）。
代价函数（cost function）
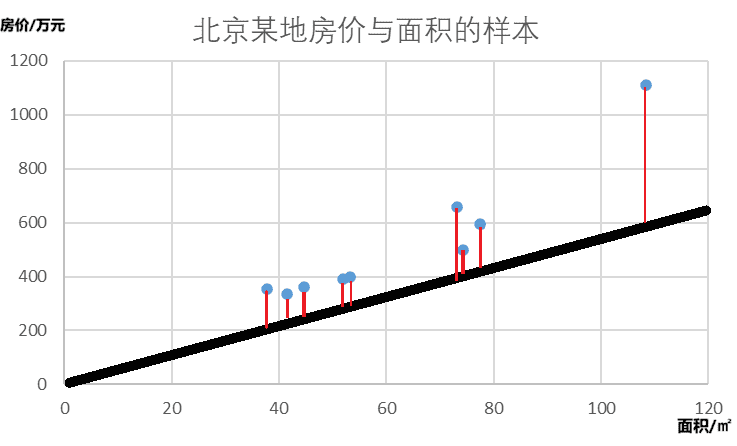
可以通过求线上预测值和真实值的方差判断线上一点与样本的契合程度。
如果求出一个预测值和真实值的方差，就可以判断二者的契合程度好误差大小。同理，如果将每一个预测值和真实值的方差相加，便能判断整个模型与训练集的误差大小。
线性回归的代价函数被定义为
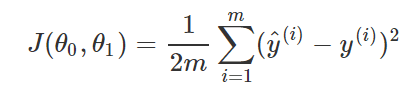
公式中的m为feature的总量。y(i)表示第i个y值。计算方法为：对总量为m的预测值（线上的点）与真实值的方差求和，然后除以2m。除以2m的目的是方便后续计算，与误差大小无关。
cost function越小，模型就越符合训练集。
因此，当代价函数为最小值时，模型就为最佳回归线。