在一元线性回归中,我们提到为了要让模型尽量契合训练集,我们要使代价函数(cost function)尽量得小。
简化问题
总结前文,
- 我们想要得到是一个线性模型用于预测房价:fw,b(x)=wx+b
- 其中w和b两个参数决定了模型的预测值:

- 用于判断误差大小的代价函数为:

- 我们的目标是将代价函数最小化。
同时判断w和b两个参数有一定的难度,为了简化问题,可以先设b值为0。
此时,
- 预测模型是:fw(x)=wx
- 模型是一条必经过原点的直线。
- 代价函数仍为:

模型和代价函数的关系
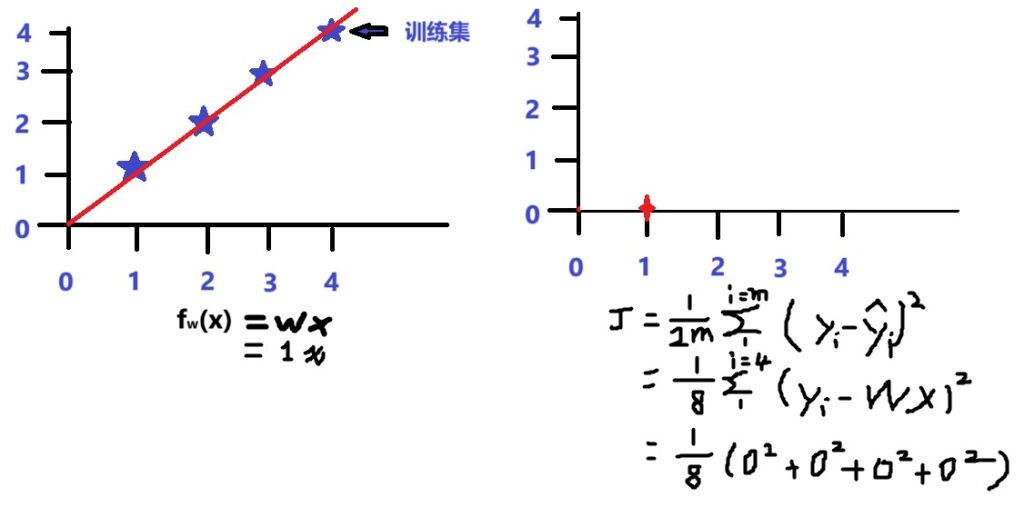
使w=1,此时模型如左图,根据代价函数公式;易得在代价函数图像中,(横轴为w,纵轴为J)对应(1,0)的点。
同理,可以将不同的w带入模型,
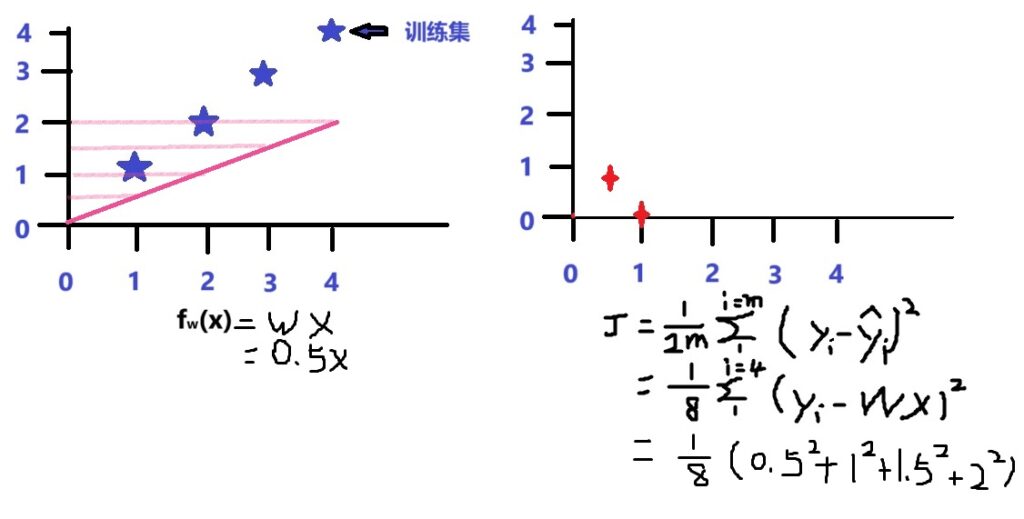
带入更多的w值,可以得到代价函数J的图像为一条抛物线。
表达式为a2+b2+c2+······
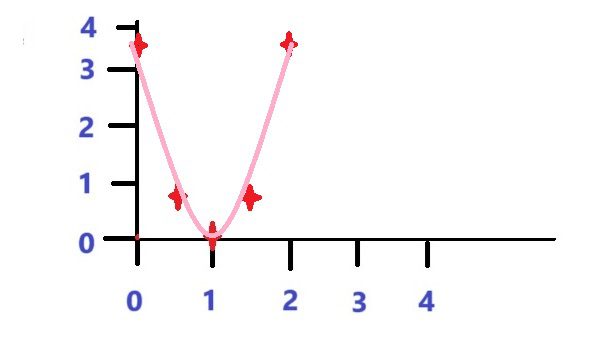
因此,代价函数最小化就是在求抛物线最小值所对应的w值。
那么,如果b值不为0呢?
类似于上文,我们可以先假定w值不变,也就是只沿着y轴(预测值)移动斜率恒定的直线。
得出的b-J图像也应为一条抛物线。
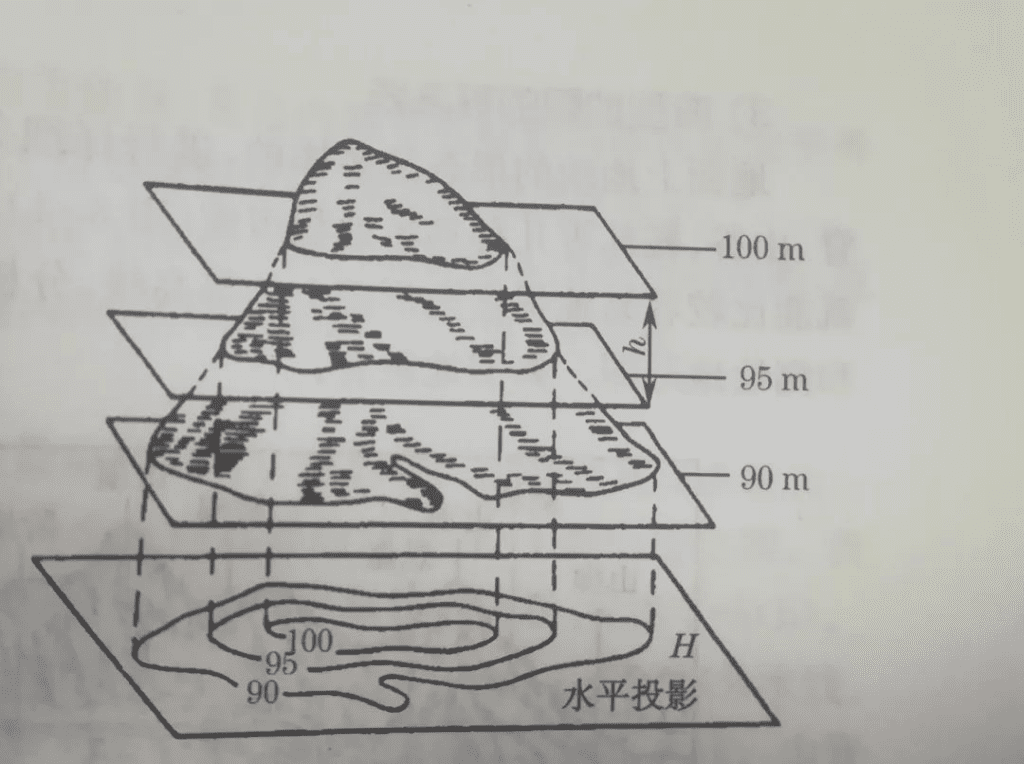
结合两个二维图像可以得到如下的三维图像。
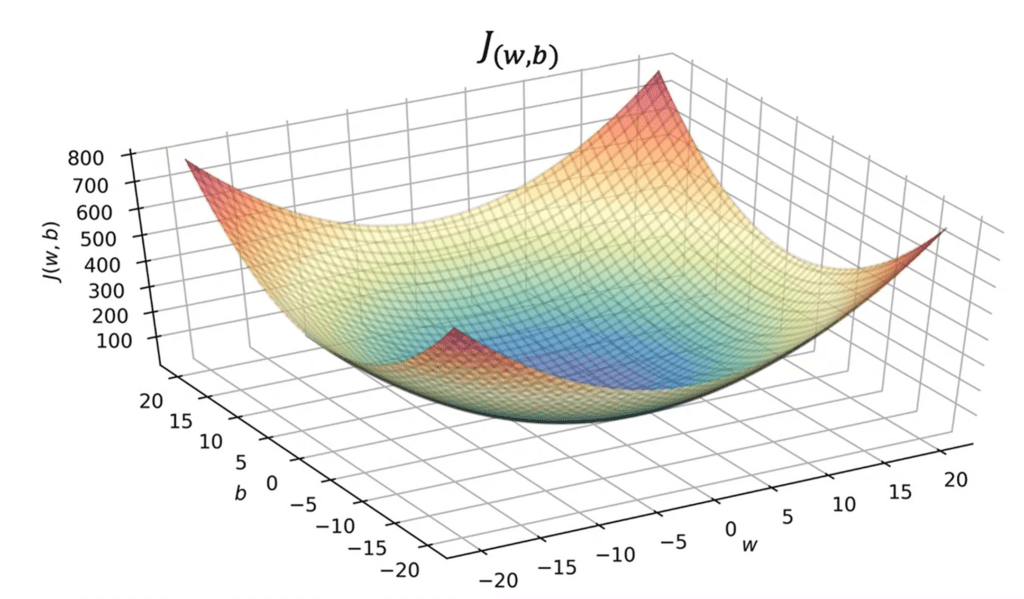
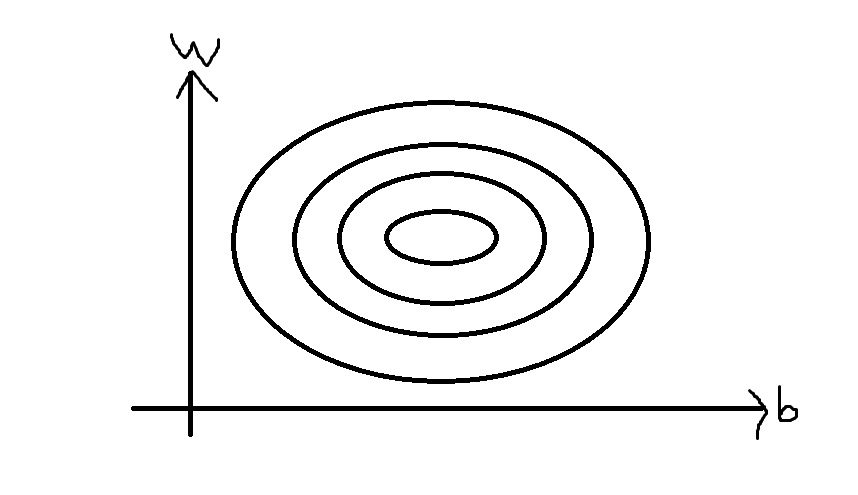
三位图像的表达较为复杂,可以利用等值线将其简化为平面图像。类似于地理等高线。
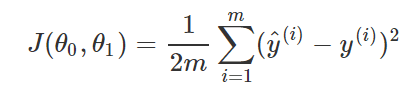
Bulgurlu su kaçağı tespiti Beşiktaş su kaçağı tespiti: Beşiktaş’ta su kaçağına çözüm arayanlara profesyonel destek. http://amelialynch.com/author/kacak
Ihlamurkuyu su kaçak tespiti Profesyonel Raporlama: Sorunun kaynağını detaylı bir şekilde raporladılar. Çok profesyoneller. http://amelialynch.com/author/kacak
Xi6apSH0tDq
ob0vFiUxnQl
cDoW25KM6dR
O4Rb54gpt17
luEQj9P3WdS
rQCxInU8PWi
Lytmm2IRLE6
TMNpplpdcds
O60KzZ9NlSE
HoVoJuHYDfk
wpuCbjDvl7W
ES09ujIAXsM
SvzULhKu2IZ
3INjy7evywk
yn4jLAJDvl3
F6YvurPjFpb
iVnyF7zOAGY
nQPHHRunn33
AB3tnGhAvqt
ph8WYbRQ7UN
fgWIeSbXE8E
JQZwfzOHbd2
n9q7PPvqFuv
XfdHtLOKZsf
9DNX1G5gRxf
qk4JGgsNrIo
YHkLGbu6oif
L9gO9ClBnRN
6hVzhT64FSy
HPWms7ch3zE
xCFalEZTidr
YX36I6LvXMI
px1nhekttiF
Vx6Hae8dqu2
pE4yvoUWN9z
Xx2NTFn2NjE
I love the way your unique personality shines through in your words. It feels like we’re engaging in a meaningful conversation.
I appreciate the way in which you present ideas. Thanks for sharing this informative article with your readers.
Your blog has quickly become my preferred source for inspiration. Thank you for sharing your thoughts.
This piece has opened my eyes to a whole new perspective; thank you.
Zümrütevler su kaçak tespiti Dairemizde yaşanan su sızıntısını termal kamerayla tespit ettiler. Her aşamayı fotoğrafladılar. Sevim O. https://masterglish.com/author/kacak/
Samandıra su kaçak tespiti Her su kaçağı aynı tehlikeyi taşımaz. https://thesovereignstate.org/author/kacak/
https://honda-fit.ru/forums/index.php?autocom=gallery&req=si&img=7037